牛顿-拉夫森法潮流计算
本文最后更新于:2025年3月27日 下午
在电力系统潮流计算中,我们需要求解非线性功率平衡方程。牛顿-拉夫森法的基本思想就是将这些非线性方程在当前点做泰勒展开,忽略高阶项,从而用雅各比矩阵来描述局部线性关系,迭代求解更新量。
实验数据
1 | |
使用牛顿-拉夫森法进行电力系统潮流计算的步骤如下:
1.形成节点导纳矩阵
根据网络拓扑和支路参数(阻抗、导纳等),构建节点导纳矩阵$Y=G+jB$,其中$G$为电导矩阵,$B$为电纳矩阵。
初始化节点电压
- PQ节点:电压幅值 $V$ 设为 $1.0 p.u.$,相角设为 0。
- PV节点:电压幅值 $V$ 设为设定值,相角设为 0。
- 平衡节点:电压幅值和相角固定,不参与迭代。
节点分类
1 | |
size(A, dim): 返回矩阵A在维度 dim 的大小(dim=1 为行数,dim=2 为列数)。find(condition): 返回满足逻辑条件 condition 的元素的索引。deg2rad(degrees): 将角度从度数转换为弧度。A(:, columns): 提取矩阵 A 的指定列(columns 可以是单列或范围)。A(rows, columns) = val: 对矩阵 A 的指定行和列赋值。
电压初始化
1 | |
功率标幺化
1 | |
- 将实际功率(MW/MVar)除以基准功率,转换为标幺值。
构建导纳矩阵
导纳矩阵描述节点之间的电气连接关系。
自导纳 $Y_{ii}$ 表示节点 $i$ 自身与所有连接的支路(包括对地导纳)的总导纳。表示当该节点电压变化时,其自身注入电流的能力。
互导纳 $Y_{ij}$ 表示节点 $i$ 与节点 $j$ 之间的电气耦合关系。
- 互导纳的负号表示电流从节点 $i$ 流出到节点 $j$ 。其绝对值即为支路导纳,反映节点间的直接电气连接强度。
导纳矩阵的本质是
节点电压方程的系数矩阵,满足基尔霍夫电流定律(KCL):
$$
I=YV
$$
计算公式为:
- 自导纳(对角线元素)
$$
Y_{ii} = \sum_{j \in \text{邻接节点}} y_{ij} + \sum_{k \in \text{接地支路}} y_{shunt,k}
$$ - 互导纳(非对角线元素)
$$
Y_{ij} = -y_{ij}
$$ - 支路导纳
$$
y_{ij}=\frac{1}{R_{ij}+jX_{ij}}
$$ - 支路对地导纳:来源于传输线路的电容效应,通常通过等效π模型描述。
$$
y_{shunt,k}=jB_{shunt,k}
$$
节点并联导纳
- 并联电导 $G_{shunt}$ 代表节点对地的有功损耗(如并联电阻)。
- 并联电纳 $B_{shunt}$ 代表节点对地的无功补偿或充电电容(如并联电容器或电抗器)。
在构造节点导纳矩阵(Ybus)时,每个节点的对角元表示该节点的“自导纳”,即所有与该节点相连的导纳之和。对于直接并联于节点的支路(或称并联支路、节点并联导纳),它们直接连接在节点与地之间,因此只影响该节点自身,不会与其他节点形成互导纳,这就要求在构造 Ybus 时把这些并联导纳直接加到该节点的对角元上。
变压器模型的导纳矩阵(变比k:1)
- 自导纳(对角线元素)
$$
Y_{ii} = \sum_{j \in \text{邻接节点}} y_{ij} + \sum_{k \in \text{接地支路}} y_{shunt,k}
$$ - 互导纳(非对角线元素)
$$
Y_{ij} = -y_{ij}
$$
Matlab实现
1 | |
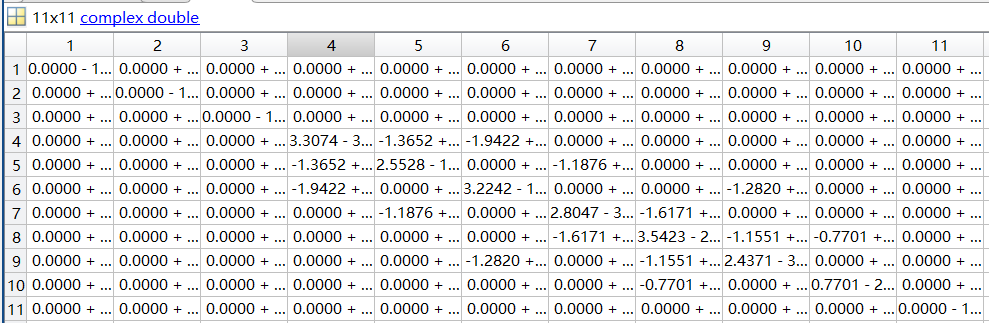
2.计算功率误差
根据当前电压值,计算各节点的注入功率$P_i$和$Q_i$,并计算功率误差:
$$
P_i = \sum_{j=1}^n V_i V_j \left( G_{ij}\cos\theta_{ij} + B_{ij}\sin\theta_{ij} \right)
$$
$$
Q_i = \sum_{j=1}^n V_i V_j \left( G_{ij}\sin\theta_{ij} - B_{ij}\cos\theta_{ij} \right)
$$
其中 $\theta_{ij} = \theta_i - \theta_j$,$Y_{ij}=G_{ij}+jB_{ij}$ 为导纳矩阵元素。
Matlab代码
1 | |
3.构建雅可比矩阵
在电力系统潮流计算中,我们需要求解非线性功率平衡方程。牛顿-拉夫森法的基本思想就是将这些非线性方程在当前点做泰勒展开,忽略高阶项,从而用雅各比矩阵来描述局部线性关系,迭代求解更新量。
对于电力系统,设功率平衡方程为:
牛顿-拉夫森迭代公式写作:
这里的雅可比矩阵 $J$,由四个子矩阵构成。
每个部分反映了功率平衡方程中各变量间的敏感度,帮助确定如何调整节点电压和相角,使得功率偏差趋于零。
雅各比矩阵的构建
- H矩阵 : $\Delta P$ 对 $\theta$ 的偏导数
$$
H_{ii} = -\left( Q_i + B_{ii} V_i^2 \right)
$$
$$
H_{ij}=V_iV_j(G_{ij}sin\theta_{ij}-B_{ij}cos\theta_{ij})
$$
$$\theta_{ij}=\theta_{i}-\theta_{j}$$
N矩阵:$\Delta P$ 对电压$V$的偏导数(仅PQ节点)
$$
N_{ii} = \frac{P_i}{V_i} + G_{ii} V_i
$$
$$
N_{ij} = V_i \left( G_{ij} \cos\theta_{ij} + B_{ij} \sin\theta_{ij} \right)
$$J矩阵 :$\Delta Q$ 对相角$\theta$的偏导数(仅PQ节点)
$$
J_{ii} = P_i - G_{ii} V_i^2
$$
$$
J_{ij} = V_i V_j \left( G_{ij} \cos\theta_{ij} + B_{ij} \sin\theta_{ij} \right)
$$L矩阵 : $\Delta Q$ 对 $V$ 的偏导数
$$
L_{ii} = \frac{Q_i}{V_i} - B_{ii} V_i
$$
$$
L_{ij} = V_i \left( G_{ij}\sin(\theta_i - \theta_j) - B_{ij}\cos(\theta_i - \theta_j) \right)
$$
理解雅各比矩阵的意义
局部线性化:
在迭代求解过程中,非线性函数在当前解附近可以被近似为线性函数,雅各比矩阵提供了这种线性近似的斜率信息。灵敏度分析:
雅各比矩阵的各个元素反映了各个变量(如电压幅值、相角)变化对功率偏差的影响程度,是进行灵敏度分析和优化的重要依据。求解更新量:
通过求解线性方程组 $J\Delta x=-F(x)$ ,可以得到下一次迭代的修正量 $\Delta x$ ,进而更新解,直至收敛。
Matlab代码
1 | |
输入参数
V: 电压幅值向量(标幺值)theta: 电压相角向量(弧度)G,B: 导纳矩阵的实部(电导)和虚部(电纳)Node: 节点数据表(含并联导纳)non_slack: 非平衡节点索引(需计算θ的节点)pq_nodes: PQ节点索引(需计算V的节点)P,Q: 节点注入功率计算值
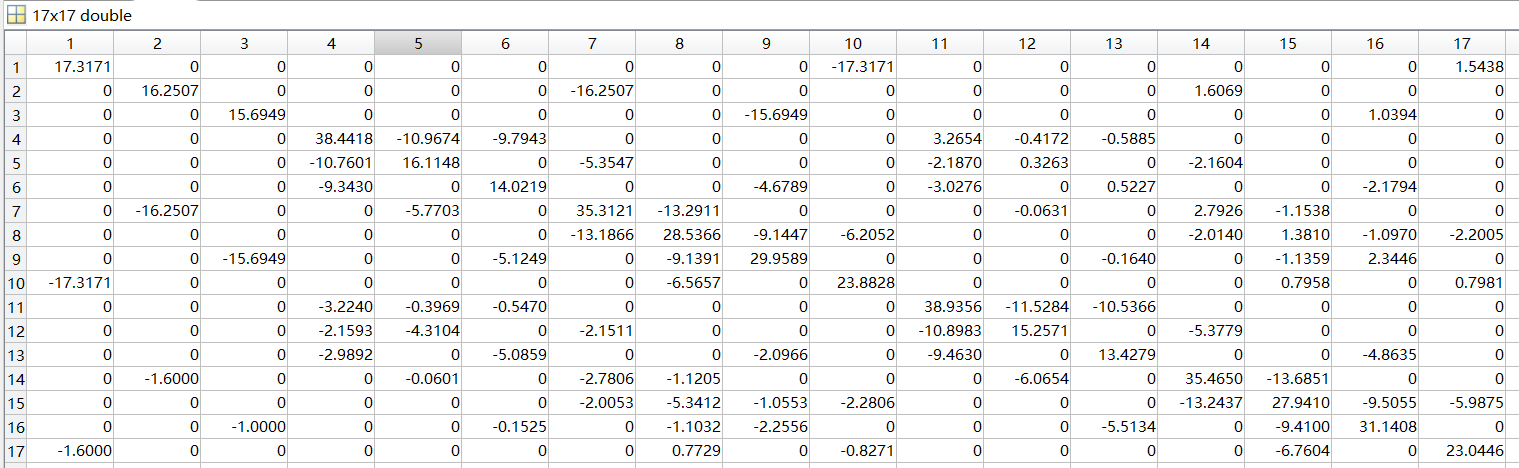
4.迭代循环
4.1 解修正方程
修正方程为:
$$
J
\begin{bmatrix}
\Delta \theta \[0.5em]
\Delta V
\end{bmatrix}=\begin{bmatrix}
\Delta P \[0.5em]
\Delta Q
\end{bmatrix}
$$
其中:
- J 是雅各比矩阵。
- $\Delta \theta$ 是相角修正量。
- $\Delta V$ 是电压幅值修正量。
- $\Delta P$ 和 $\Delta Q$ 是功率误差。
Matlab实现
1 | |
mismatch是功率误差向量,维度为 $\Delta P$ 和 $\Delta Q$ 的拼接。- MATLAB的
\运算符会自动选择高效的数值方法(如LU分解)求解线性方程组。
- MATLAB的
计算功率误差向量
1 | |
4.2 更新变量
理论公式:
$$
\theta^{(k+1)}=\theta^{k}+\Delta \theta
$$
$$
V^{(k+1)}=V^{k}+\Delta V \quad \text{仅PQ节点}
$$
- PQ节点:电压幅值 $V$ 设为 $1.0 p.u.$,更新相角和幅值。
- PV节点:电压幅值 $V$ 设为设定值,仅更新相角。
- 平衡节点:电压幅值和相角固定,不参与更新。
Matlab实现
1 | |
4.3 收敛判断
理论条件:
若所有功率误差的绝对值小于预设阈值(例如预设阈值为 $\epsilon=10^{-5}$ ),则收敛。
$$
\max (|\Delta P|,|\Delta Q|)<\epsilon
$$
不收敛,则返回第三步。
Matlab实现
1 | |
完整的迭代循环
1 | |
注释
~converged:~是逻辑非运算符,表示取反。
5.更新节点数据
1 | |
6. 结果评价(检验)
收敛只是验证算法在数值上达到了某种收敛标准,但这并不一定意味着计算结果在物理和工程上是正确的。
PQ 节点功率注入接近零:
对于 PQ 节点来说,它们的指定功率通常为“发电 - 负荷”。
如果一个 PQ 节点没有装机发电机(也就是说只有负荷),那么它的指定功率就是 发电 − 负荷
- 在潮流计算中,计算出来的功率注入 $𝑃$ 应该与这个指定值一致,也就是计算得到的 $𝑃$ 应该接近
− 负荷。- 当把“指定功率减去计算功率”的不平衡量 $\Delta P$ 计算出来时,它会接近零。
- 这表明在该节点,实际计算出来的功率注入与负荷完全匹配,没有多余或不足的功率误差。
平衡节点吸收剩余功率:
平衡节点(Slack 节点)的作用是为整个系统提供一个参考,其电压和相角通常被固定,且它承担系统中所有未被其他节点平衡的功率。
- 所有 PV 和 PQ 节点的功率注入总和加上平衡节点的功率注入应该满足功率平衡(即总发电等于总负荷加上线路损耗)
- 如果其他节点已经严格平衡(即它们的计算功率与指定功率差值很小),那么系统的总功率不平衡主要体现在平衡节点上。平衡节点的功率计算值就会等于“剩余”未平衡的那部分功率,从而保证整个系统的功率平衡。
具体分析
在潮流计算中,每个节点的有功注入定义为
$$
P_i = P_{\text{gen},i} - P_{\text{load},i},
$$
其中 $P_{\text{gen},i}$表示节点 (i) 的发电机出力,有功负荷 $P_{\text{load},i}$ 通常为正值,因此对于仅负荷的 PQ 节点,指定的功率为
$$
P_{\text{spec},i} = - P_{\text{load},i}.
$$
对于所有非平衡节点(即所有 PV 和 PQ 节点),它们的总有功注入为
$$
P_{\text{total, non-slack}} = \sum_{i \in \text{PV}} \left(P_{\text{gen},i} - P_{\text{load},i}\right) + \sum_{i \in \text{PQ}} \left(P_{\text{gen},i} - P_{\text{load},i}\right).
$$
本例的数据中,节点类型分别为:
- PV 节点:节点 1、2、3
- PQ 节点:节点 4、5、6、7、8、9、10
- Slack 节点:节点 11
1. PV 节点
根据数据:
| 节点 | $P_{\text{gen}}$ (MW) | $P_{\text{load}}$ (MW) |
|---|---|---|
| 1 | 160 | 0 |
| 2 | 160 | 0 |
| 3 | 100 | 0 |
因此,
$$
P_{\text{spec},1} = 160,\quad P_{\text{spec},2} = 160,\quad P_{\text{spec},3} = 100.
$$
PV 节点总和为
$$
\sum_{i\in \text{PV}} P_{\text{spec},i} = 160 + 160 + 100 = 420 , \text{MW}.
$$
同理,
$$
\sum_{i\in \text{PV}} Q_{\text{spec},i} = 30 + 50 + 50 = 130 , \text{MW}.
$$
2. PQ 节点
对于 PQ 节点(无发电机出力),根据数据:
| 节点 | $P_{\text{gen}}$ (MW) | $P_{\text{load}}$ (MW) |
|---|---|---|
| 4 | 0 | 0 |
| 5 | 0 | 200 |
| 6 | 0 | 230 |
| 7 | 0 | 0 |
| 8 | 0 | 200 |
| 9 | 0 | 0 |
| 10 | 0 | 0 |
所以,
$$
P_{\text{spec},4} = 0,\quad P_{\text{spec},5} = -200,\
P_{\text{spec},6} = -230,\quad P_{\text{spec},7} = 0,\quad\
P_{\text{spec},8} = -200,\quad P_{\text{spec},9} = 0,\
P_{\text{spec},10} = 0.
$$
PQ 节点总和为
$$
\sum_{i\in \text{PQ}} P_{\text{spec},i} = -200 -230 -200 = -630 , \text{MW}.
$$
同理,
$$
\sum_{i\in \text{PQ}} Q_{\text{spec},i} = -80 -77 -77 = -227 , \text{MW}.
$$
3. 非平衡节点总和及 Slack 节点补偿
将 PV 和 PQ 节点的总和相加,
$$
P_{\text{total, non-slack}} = 420 + (-630) = -210 , \text{MW}.
$$
$$
Q_{\text{total, non-slack}} = 130 + (-227) = -97 , \text{MW}.
$$
这意味着所有非平衡节点(PV+PQ)整体需要消耗 210 MW 的有功功率和-97 MW 的无功功率。
为了实现全系统功率平衡,总功率应满足
$$
\sum_{i=1}^{N} P_i = 0.
$$
$$
\sum_{i=1}^{N} Q_i = 0.
$$
因此,Slack 节点必须补偿这一缺口,提供约
$$
P_{\text{slack}} \approx -\left(P_{\text{total, non-slack}}\right) \approx 210 , \text{MW}.
$$
$$
Q_{\text{slack}} \approx -\left(Q_{\text{total, non-slack}}\right) \approx -97 , \text{MW}.
$$
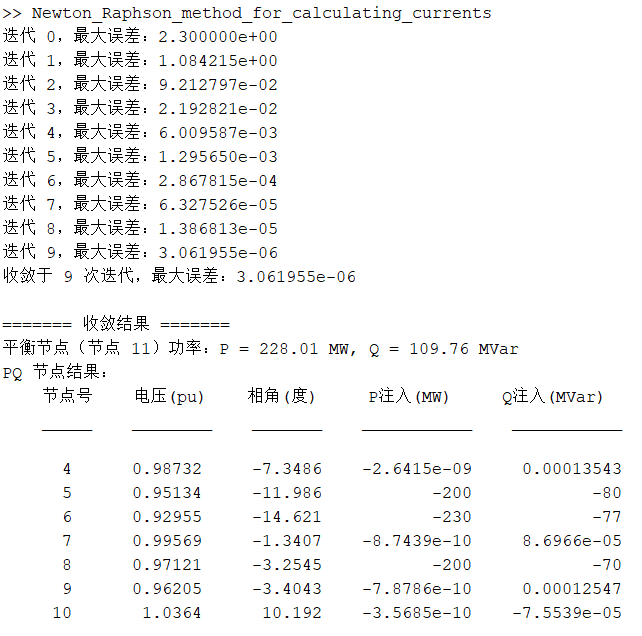
计算得到的Slack 节点显示:
$$ P = 228.01 MW $$
$$ P = 109.76 MW $$
这可能由于线路损耗或数值误差导致略有差异,但整体上符合系统平衡的要求。
markdown 表格居中
现在.md文件的开头插入:
1 | |
然后在需要居中的表格:
1 | |